2017. 4. 6. 21:10ㆍmachine learning
TensorFlow를 이용해서 선형 회귀 분석을 해 볼 것이다.
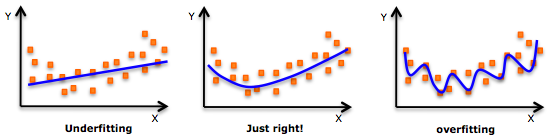
우선 우리는 주어진 데이터에 대해서 가장 알맞는 input/output를 출력하는 함수 f를 찾아낼 것이다. f를 찾기 위해서 고려할 사항이 두 가지가 존재하는데 바로 variance와 bias이다. - variance는 주어진 training set에 대해서 찾아낸 함수 f가 얼마나 민감한가를 나타내는 척도이다. overfitting(입력 데이터에 대해서만 아주 정확하게 결과를 출력하는 경우) 인 경우에 대부분 variance가 높게 나타나는데, variance가 높은 경우 약간의 입력 데이터 변화만 생기더라도 오답을 출력하는 문제가 발생한다. 그래서 우리는 variance를 낮출 필요가 있다.- bias는 훈련 데이터에 대한 편견을 나타낸다. 주어진 훈련 데이터에 대해 일정 기준을 정하는 것이다. 예를 들어 어느 반 학생들의 키가 주어진 데이터라고 했을 경우에 우리는 함수 f를 찾을 때 '다들 150cm 보다는 클거야' 라는 bias를 둠으로써 해당 f함수에 대한 추가 규제를 둘 수가 있다. 너무 높은 편견을 세우게 되면( ex) 180cm 보다 클거야) 주어진 데이터에 대한 일반화가 어려워지기 때문에 보다 낮은 bias를 선호한다.결과적으로 우리는 함수 f를 찾을 때 낮은 variance와 낮은 bias를 가지는 모델을 찾아야 할 필요가 있다.
그럼 이제 아래 코드를 통해 linear regression을 살펴보자.
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
learning_rate = 0.01training_epochs = 100
x_train = np.linspace(-1, 1, 101)y_train = 2 * x_train + np.random.randn(*x_train.shape) * 0.33
X = tf.placeholder("float")Y = tf.placeholder("float")
def model(X, w):return tf.mul(X, w)
w = tf.Variable(0.0, name="weights")
y_model = model(X, w)cost = (tf.square(Y-y_model))train_op = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
sess = tf.Session()init = tf.global_variables_initializer()sess.run(init)
for epoch in range(training_epochs):for (x,y) in zip(x_train, y_train):sess.run(train_op, feed_dict={X:x, Y:y})w_val = sess.run(w)
sess.close()plt.scatter(x_train, y_train)y_learned = x_train * w_valplt.plot(x_train, y_learned, 'r')plt.show()
우선 np.linspace(-1, 1, 101)을 통해 -1부터 1사이의 균일 간격의 101개의 숫자 리스트를 x_train에 생성한다.예) [-1, -0.98, -0.96, ......., 1]이제 train에 대한 결과 값을 생성해야 하는데, 그걸 위해 y_train이라는 변수를 아래의 처리 방식으로 만들어 주자.
y_train = 2 * x_train + np.random.randn(*x_train.shape) * 0.33
x_train에 2를 곱한 다음 임의의 random_number를 생성한 후 * 0.33을 곱한 값을 더한 결과가 y_train이 된다.
random.randn 파라미터에 *가 들어가 있는 것은 해당 인자를 unpack하기 위한 용도이다. 아래의 예를 살펴보면 이해가 쉬울 것이다.
args = [3, 6]list(range(*args))
위의 예제에서는 args가 unpack이 되어서 range의 start 인자에 3이 end 인자에 6이 들어가게 된다. y_train의 random 함수도 같은 방식이 적용되서 101개의 랜덤 변수 리스트를 생성하게 된다.
실제로 session.run을 할 때, 변수를 입력할 변수 저장 공간을 X,Y란 placeholder로 만들어주고, 우리가 찾을 모델 방정식도 만들어 준다.
여기서는 y = wx라는 모델을 정의했고, 우리는 x_train 값이 입력으로 들어왔을 때 y_train 값을 가장 잘 설명해 줄 수 있는 w 값을 찾아내면 되는 것이다.
w의 초기 값은 0으로 설정을 해주고, cost 함수도 정의를 해준다. cost 함수는 y의 실제 값에서 우리가 예측한 예측 값을 뺀 후의 제곱을 취한 값(MSE)으로 설정을 하는데, 이 후에 gradient_descent_optimizer에서 해당하는 cost의 값이 가장 작아지는 지점을 찾음으로써 w값을 찾아나가게 된다.
이제 graph를 실행시키기 위한 모든 operator와 variable 설정이 끝났고 session을 실행시켜서 돌려보도록 하자.
for문을 python zip 함수를 통해 x_train과 y_train의 각각의 pair를 가져오고 해당 값을 feed_dict에 넣는다.
이렇게 하면 내부적으로 해당 x와 y가 들어왔을 때 x와 w를 곱한 값과 y값의 차의 제곱을 구해서 cost를 구하고 해당 cost가 0이 될 수 있도록 w값을 업데이트를 한다.
현재 위의 소스에서는 이 과정이 for문의 한 step이며, 이렇게 하는게 가장 이상적인 방식이지만 계산 또는 시간 비용을 줄이기 위해 batch란 개념을 둬서 한꺼번에 여러 개의 x,y값을 input으로 받고 각각 cost 결과의 평균을 구한 뒤 해당 평균이 0이 될 수 있도록 w를 업데이트 하는 방식이 현재로썬 가장 많이 사용된다.
for문이 종료되면 w_val 값에는 cost가 0에 가까운 값을 낼 수 있도록 하는 가중치 값이 계산이 되었을 것이다.
이제 plot 함수를 써서 x와 y의 2차원 데이터 분포를 그림으로 표현해본다.
그 후에 우리가 계산한 w_val에 x_train 값을 곱한 결과 그래프를 빨간 선으로 표시해 보자.
